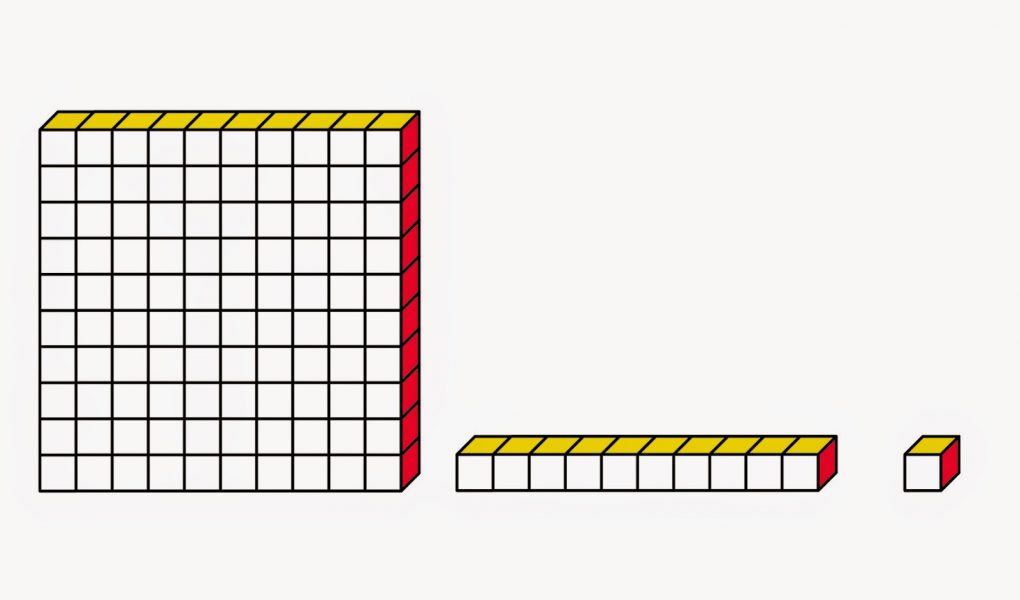
La base de 10
Dans le système décimal, la base de 10 est aujourd’hui la référence dans le domaine des sciences.
Qu’est-ce-qu’une base de calcul ?
En arithmétique, une base correspond à des valeurs successives (=nombres) définissant un ordre de grandeur. Chaque valeur est représentée par un chiffre. Ici, dans la base de 10, nous y retrouvons tous les nombres allant de 0 à 9 ; ce qui correspond à l’unité.
La base de 10 : qu’est-ce-que c’est ?
La base de 10, aussi appelée système décimal, est un principe de numération mathématique qui consiste à organiser une collection d’objets à dénombrer, en les regroupant par paquets de dix; par paquets de dix dizaine (=centaines), etc. Il peut être appliqué sous forme de tableau avec les unités, les dizaines (10 1 ), les centaines (10 2 ), les centaines (10 3 ), les milliers (10 4 ), etc.
Grâce à un tableau, nous nous rendons compte que, dans chaque case, les chiffres indiqués sont forcément inférieur à 10. Par ailleurs, si nous remarquons une absence de chiffre dans l’une des cases, nous y plaçons automatiquement un 0. Ainsi, grâce à la base 10, nous pouvons décomposer n’importe quel nombre de façon très simple.
Par exemple : 23 456 = (2 x 10 000) + (3 x 1 000) + (4 x 100) + (5 x 10) + 6.
La base 10 est l’une des bases les plus utilisées dans le monde et ce, depuis des millénaires.
Elle est dictée par l’utilisation des 10 doigts de la main, ce qui permet de faciliter les calculs.
Par exemple, au IIIème Millénaire avant J-C, les Egyptiens utilisaient déjà ce système ; suivirent les Chinois en -1350 (十 = 10, 二十 = 20, 三十 = 30, 四十 = 40), en -650 les Etrusques (centre de la Péninsule Italienne) et en -500 les Indiens à travers le Sanskrit (langue Indo-Européenne).
Bien que cette base de 10 soit désormais très courante partout dans le monde, mais cela n’a pas toujours été le cas. Des bases anciennes encore présentes dans la vie de tous les jours.
Les Babyloniens, eux, utilisaient une base 60, appelée système séxagésimal. Nous retrouvons encore ce système notamment dans l’heure (60 minutes), mais aussi en géométrie (360° pour un cercle). La base de 12, appelée système duodécimal, était aussi utilisé par les Egyptiens pour exprimer les heures (12 heures) et les mois. Enfin, la base 20, aussi appelé système vicésimal, était très utilisé par les Mayas, les Aztèques, mais aussi durant les premiers temps de l’Europe. Nous avons hérité de cette base 20, notamment avec le nombre quatre-vingt (80).
Comme quoi, de nombreuses bases ont sû être conservées malgré le temps, et sont toujours très importantes dans la vie quotidienne. Etonnant, non ?
Les nouvelles bases
L’une des bases les plus utilisées aujourd’hui, en plus de la base 10, est la base 2. Appelée aussi système binaire cette base est surtout utilisée dans de nombreux systèmes électriques comme les calculatrices, les circuits électriques, mais aussi en informatique. Dans le système binaire, la base 2 est représentée par 0 et 1, c’est-à-dire qu’il n’y a que deux états utilisés.
Bien avant de l’apparition du premier ordinateur, deux grandes têtes pensantes se sont davantage penchées sur la question : Gottfried LEIBNIZ (1646-1716) et George BOOLE (1815- 1864). LEIBNIZ aurait découvert le système binaire grâce à un traité chinois datant 750 avant J-C : le Yi Jing. En se basant sur ce traité chinois, il aurait écrit son propre manuscrit “De Progessione Dyadica”. Comme nous pouvons le constater, le système binaire a été créé bien avant l’invention de l’ordinateur et des appareils électroniques !
Quant à BOOLE, il a créé l’Algèbre de BOOLE dans lequel il reprend le système binaire pour décrire les valeurs de vérité. Nous retrouvons cette algèbre dans de nombreuses applications informatiques et dans la conception de circuits électriques. Cette partie du programme de maths est notamment étudiée en début d’année de prépa maths sup à l’école.